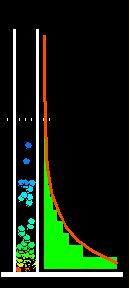
The animation (mpg, 0.9 Mo) shows an ideal gas in a constant gravitational field: 50 particles with the same mass are initially uniformly distributed between the bottom of the box and the dashed line.
2. Solar Atmosphere (Filippo Pantellini)
50 Particles: what distribution for density and velocities?

The animation
(mpg, 0.9 Mo) shows an ideal gas in
a constant gravitational field: 50 particles with the same mass are initially
uniformly distributed between the bottom of the box and the dashed line.
The gas then evolves freely under the action of the gravitational field.
Collision rules: two
particles collide when their respective height is the same.
The system is thus in fact one-dimensional even though
their velocities have three components.
Collisions are elastic
and
the velocity distribution after a collision is assumed isotropic.
The simulation lasts a total of 50000 collisions.
To the right of the box a
"dynamic" histogram counts the number of times a particle has been observed
in the corresponding heigth interval: this gives a measurement of the density.
The red curve represents
the time-averaged density profile.
(After some time, the profile decreases exponentially
as expected from the barometric law and the virial theorem which predicts
that the average potential energy per particle equals 2/5 of the total
energy per particle)
The total duration of the simulation is 17.6 the free fall time from the top of the box.
The simulation shows that this simple model reproduces correctly the behaviour of an ideal gas in a gravitational field.
DISCUSSION: is this experiment a toy?
1. In the case of an atmosphere made of neutral particles (no charge) the solution is known... The simulation shows that 1 spatial dimension is enough to recover the solution, which opens interesting perspectives, because 1 dimension is accessible to present-day computers, not three dimensions.
2. In the case of the solar atmosphere (corona) the solution is unknown. The gas is almost non collisional, particles are charged with various masses (protons and electrons), and one observes an paradoxical temperature profile: temperature is low close to the heat source (the sun)...
3. A medium with few collisions , this means that the velocity distribution can deviate much from the Maxwell law which describes correctly only the case with frequent collisions.
4. Depending on the velocity distrtibution, the heat transport between the hot corona and the cold solar surface.proceeds correctly or not... Some authors suggest that the heat transport could proceed from the cold sun to the hot corona (if the velocity distribution were bizarre enough). This would "solve" the question of the coronal heating.
5. The problem is that we don't know the shape of the distribution of particle velocities in the corona and how much they deviate from a Maxwellian. Preliminary results indicate the heat flux from the corona to the sun could be weaker than previously assumed.